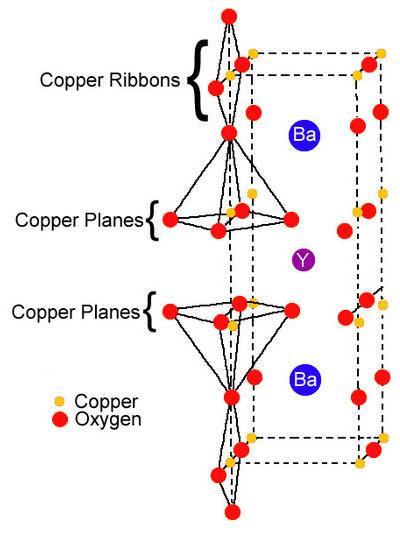
There are many oxides that have interesting properties. For example, the collosal magnetoresistance manganites and the cuprate superconductors. Oxide compounds are often have very strong Coulomb repulsion between electrons, and can have strong electron-phonon interactions. The figure shows the structure of YBCO, which is a high temperature superconductor. I have worked on understanding how electron-phonon interactions can lead to unconventional superconductivity, and on the transitions between metallic and insulating behaviour in strongly correlated materials. Investigation of these phenomena involves the application of many-body quantum theory.

Electron-phonon interactions and superconductivity

My main contribution to this field is the development of an extended Migdal-Eliashberg technique which includes vertex corrections and spatial fluctuations. In particular, I showed how vertex corrections are essential to describe the quasi-2D normal state of the Holstein model. In particular, a kink reminiscent to that in the Cuprates is seen, which is best attributed to higher order corrections. I have also extended the theory of superconductivity to quasi-2D. This is closely related to the subject of my PhD thesis (Tuning correlation effects with electron-phonon interactions, and breakdown of Migdal-Eliashberg theory). The most recent result from this project have shown that a d-wave state can be induced from the vertex corrections.

Recently, we carried out variational Monte Carlo simulations which demonstrated the stability of a d-wave state in a Hubbard-Froehlich model.

Superconductors have some incredible properties, such as magnetic levitation

Superlight small bipolarons

I also collaborate with Pavel Kornilovitch, Sasha Alexandrov and John Samson on continuous time quantum Monte-Carlo calculations of polarons and bipolarons (including the Holstein and lattice Froehlich models). We have discussed the effects of lattice geometry on polaron properties. We are now simulating bipolarons, and have concentrated on the search for super-light bipolarons in the presence of strong coulomb repulsion and for bound states with angular momentum

. Recently, we investigated the effects of impurities on polarons.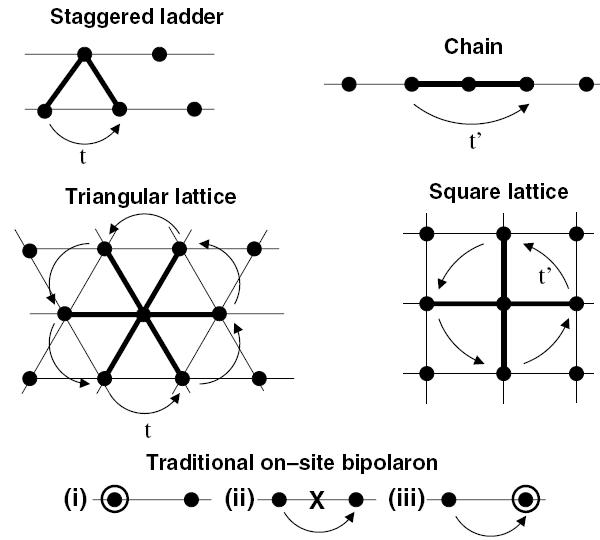

Superlight small bipolarons should be stable on a variety of lattices

Hubbard models and strong electronic correlation

Hubbard models are the standard for the study of electronic correlation. Behaviour includes a Mott transition at half-filling, antiferromagnetism, spin-charge separation, and possibly superconductivity. Often the single band model is studied, and is a good test bed for new techniques. However, what happens beyond the simplified one-band case is debated. I have studied the two-band model to investigate the differences with the one-band model. In particular, the Mott transition at half-filling is suppressed, leading to a critical coupling which is nearly 8 times larger than that required to open a gap in the one band model. This casts doubt on the existence of Mott insulators in real materials, instead suggesting that very strongly correlated band insulators, or charge transfer gap insulators should be the most common types of insulator.

Jim Hague is a Senior Lecturer in Physics at the Open University in the UK. His main research interest is many body physics (both quantum and classical). He works on problems in biophysics, condensed matter theory and cold atoms. Jim teaches a wide range of physics topics, including relativity theory, electromagnetism and quantum physics.
If you are interested in doing a PhD in this area, please consult the Department of Physical Sciences website.
These pages are the personal responsibility of J.P.Hague. The views expressed here do not necessarily represent the views of the Open University. The University takes no responsibility for any material on these pages. Last update 8th November 2017.